Move your sprite from A to B, and then from B to C.
I'd do it by adding a variable "last point reached", with the index in the vector of the point you started at (e.g. you start at A (0), go to B(1), then C(2)...)
The problem is that in "while loop" sprite instantly moves from one point to another. I want it to move smoothly to the next point.
A point (A, B...) is just two coordinates.
Let's say A has coordinates [aX, aY] and B has coordinates [bX, bY]:
The point between A and B (let's call it C) would have for coordinates:
[(aX + bX) / 2, (aY + bY) / 2]
[ A - - - | - - - | - - - | - - - | ]
[ | - - - | - - - C - - - | - - - | ]
[ | - - - | - - - | - - - | - - - B ]
If you want to get the point (let's call it D) between A and B, at 25% (distance between the point D and A is 25% of the length between A and B), D would have for coordinates:
[(aX * 75 + bX * 25) / 100, (aY * 75 + bY * 25) / 100]
[ A - - - | - - - | - - - | - - - | ]
[ | - - - D - - - | - - - | - - - | ]
[ | - - - | - - - | - - - | - - - | ]
[ | - - - | - - - | - - - | - - - B ]
Now if you want ANY point between A and B, at x% (x is a number between 0 and 100, where 0 means exactly over A and 100 means exactly over B), you would use this formula to get those coordinates:
[(aX * {100 - x} + bX * x) / 100
, (aY * {100 - x} + bX * x) / 100
]If you use this formula a lot, you can (and should) use x between 0 and 1, replacing every "100" with "1" and remove the "/ 100" so you do less operations.
So if you want to smoothly move from A to B, you'd use this formula at different percentages. You'll always have "teleportation" (instantly moving), but it will be so small that it'll look very smooth:
 MORE ADVANCED MATHS WITH SMOOTH CURVES
MORE ADVANCED MATHS WITH SMOOTH CURVESBezier curves:
https://en.wikipedia.org/wiki/B%C3%A9zier_curveQuadratic:
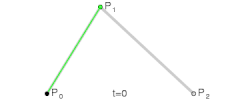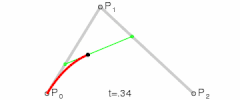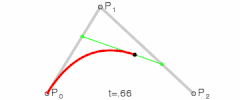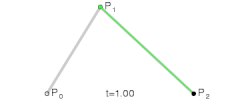
Cubic (these will make any path you can imagine):
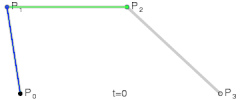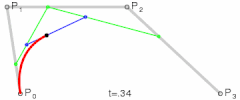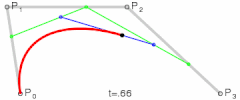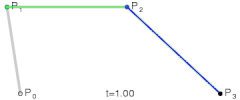
There are other "higher-order" curves, but I don't recommend using them as cubic curves already allow you to make any curved path.
You can also research other kinds of curves, there are many and they may make your "path" look smoother and less abrupt, but you'll
HAVE to deal with math.




